A stationary wave is formed when two progressive waves travelling in opposite directions combine to form a fixed pattern that remains over time.

If a stationary wave is formed there will places where the amplitude is zero called nodes. The nodes do not move. There are also places of maximum amplitude called anti-nodes. The magnitude of displacement at an anti-node changes with time not position.

The stationary only exists at definite frquencies. The lowest frequency at which a stationary wave forms is called the fundamental mode or first harmonic.

The distance between two adjacent nodes is always \( \frac{\lambda}{2} \).

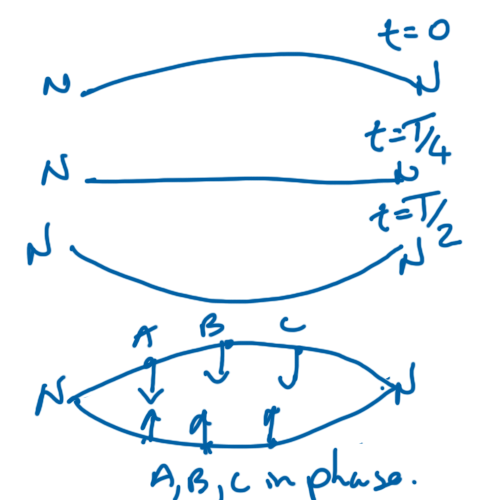
The fundamental mode is formed when there are only two nodes and one anti-node. The distance between the nodes is \( \frac{\lambda}{2}\).

The frequency of the fundamental is given by:

$$ f = \frac{v}{2L} $$

Where L is the distance between the nodes.

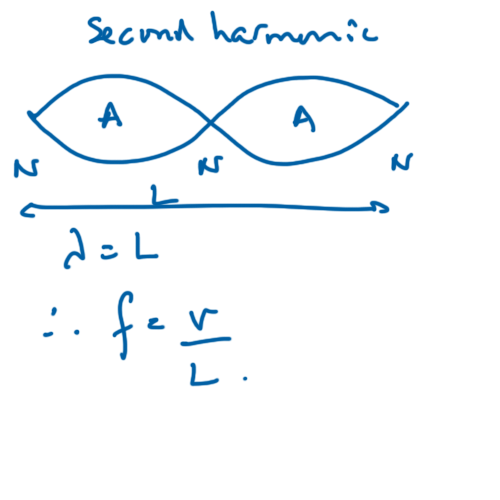
The second harmonic is formed when a complete wavelength fits between the ends and the are three nodes and two anti-nodes.

The frequency of the second harmonic is given by:

$$ f = \frac{v}{L} $$

Which is

$$ f_2 = f_1 \times 2 $$

and in general

$$ f_n = f_1 \times n $$

for the nth harmonic

The speed of waves on a string under tension is given by:

$$ v = \sqrt{\frac{T}{\mu}} $$

So the frequency is:

$$ f = \frac{1}{2L}\sqrt{\frac{T}{\mu}} $$

The second harmonic is given by:

$$ f_2 = 2 \times f_1 $$

Which is

$$ f_2 = \frac{1}{L}\sqrt{\frac{T}{\mu}} $$

and in general

$$ f_n = \frac{n}{2L}\sqrt{\frac{T}{\mu}} $$

for the nth harmonic

and the length of the string is such that:

$$ L = \frac{n \lambda}{2} $$

When a guitar string is plucked it produces a note governed by the first harmonic of the string.

The other harmonics at higher frequncies are present to a lesser degree. The pattern of harmonics present give the quality or timbre of the instrument and are effected by the way the instrument is made.

To mimick an instrument electronically this pattern of harmonics needs to be reproduced by adding the correct series of amplitudes for each harmonic. Any waveform can be constructed by adding particular magnitudes of the higher harmonics, This is done in electronic synthesisers and computer audio.