Optics
Refraction of light
Definition of Refraction
Refraction occurs when light changes speed and direction passing from one transparent medium to another. Usually we demonstrate this with air into glass using a glass prism. The simple way of predicting the behaviour of a light ray passing from air into glass is to say the light bends towards the normal as it goes from air into glass.
A more general approach is to use Snell's Law to predict the direction qunatitatively.
Speed of light
The speed of light in a vacuum is 299,792,458 m/s. Generally, using \(3 \times 10^8\) m/s is accepted. The speed of light in air is very similar 299,702,547 m/s, which is again accepted as \(3 \times 10^8\) m/s.
The speed of light is always slower in a transparent medium than in a vacuum. For instance \( \; c_{glass} = 2.0 \times 10^8 \; m/s \) to 2 decimal places.
$$\begin{array}{|c|c|} \hline \text{material} & \text{speed (m/s)} & \text{n, refractive index} \\ \hline
\text{air} & 2.997 \times 10^8 & 1.0003 \\ \hline
\text{water} & 2.554 \times 10^8 & 1.33 \\ \hline
\text{glass} & 1.999 \times 10^8 & 1.50 \\ \hline
\text{diamond} & 1.199 \times 10^8 & 2.50 \\ \hline
\end{array}$$
Refractive index
The refractive index is defined as the ratio of the speed of light in a vacuum to the speed of light in a transparent medium. It is always greater than 1.
$$n_{medium} = \frac{c_{vacuum}}{c_{medium}}$$
For example if we take n = 1.42 then
$$ \displaylines{c_m = \frac{c_v}{n_m} \\
c_m = \frac{3 \times 10^8}{1.42} \\
c_m = 2.11 \times 10^8}
$$
Snell's Law
NOTE: ALL angles mesaured from the NORMAL. Always identify the NORMAL first and draw on diagram before attempting any calculations.
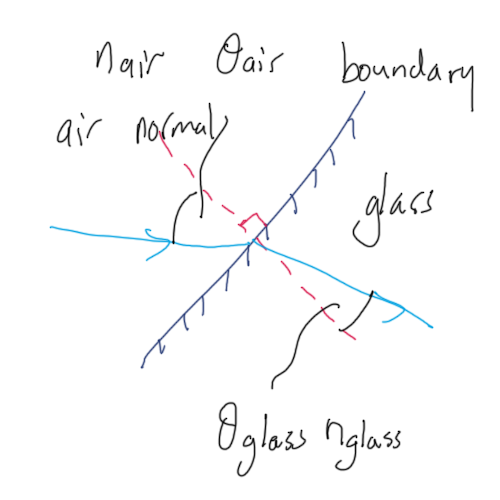
$$ n_{glass} = \frac{\sin \theta_{air}}{\sin \theta_{glass}} $$
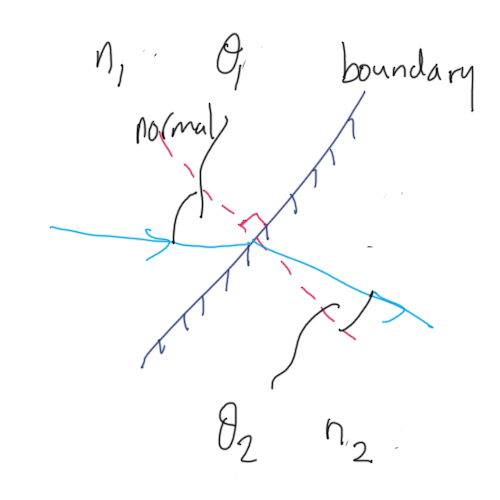
$$ _1n_2 = \frac{\sin \theta_1}{\sin \theta_2} $$
Example: Light incident on air glass boundary at 30 degrees to the normal. Find the angle of refraction in glass.
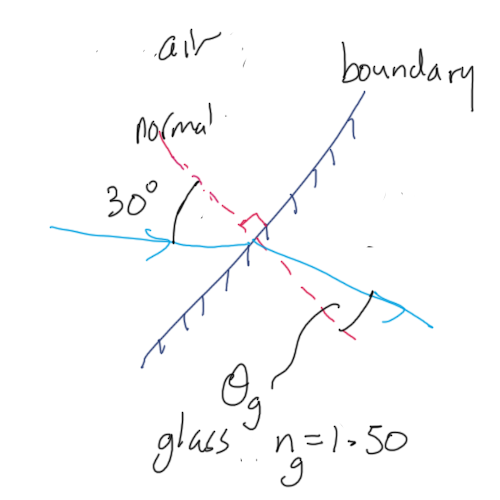
Solution:
$$
\displaylines{
\sin \theta_{glass} = \frac{\sin \theta_{air}}{n_{glass}} \\
\sin \theta_{glass} = \frac{0.5}{1.50} \\
\sin \theta_{glass} = 0.33 \\
\theta_{glass} = 19.47\textdegree
}
$$
Snell's Law
NOTE: ALWAYS use this version of Snell's Law solving A-level calculations.
$$ n_1 \times \sin \theta_1 = n_2 \times \sin \theta_2 $$

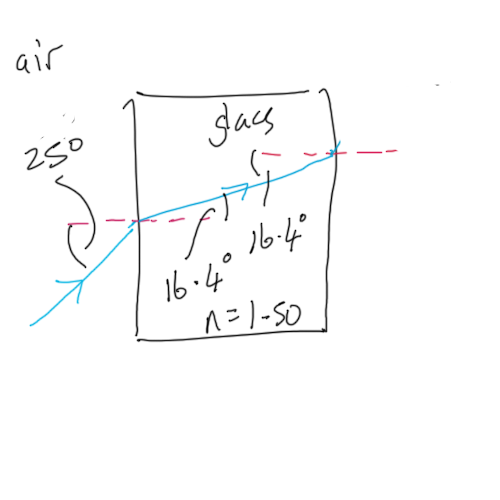
Example: Light incident on a glass block at 25 degrees to the normal. Complete the path showing all angles as it passes through the block of glass (n=1.50).
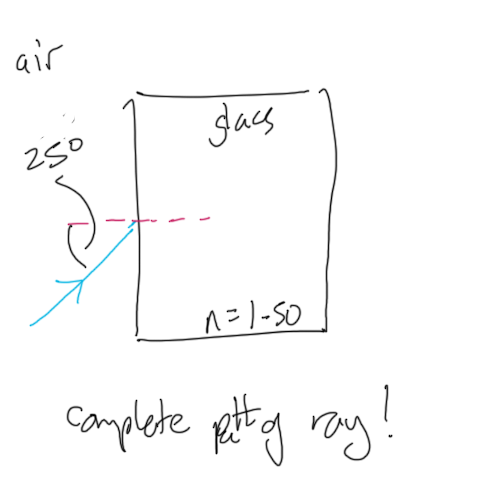
Solution: air to glass
$$
\displaylines{
n_1 \times \sin \theta_1 = n_2 \times \sin \theta_2 \\
1.00 \times \sin 25 \textdegree = 1.50 \times \sin \theta_2 \\
\sin \theta_2 = \frac{1.00 \times 0.42}{1.50} \\
\sin \theta_2 = 0.28\\
\theta_2 = 16.4 \textdegree
}
$$
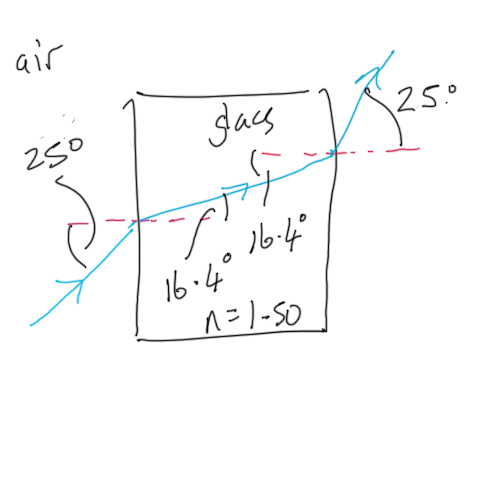
Solution: glass to air
$$
\displaylines{
n_1 \times \sin \theta_1 = n_2 \times \sin \theta_2 \\
1.50 \times \sin 16.4 \textdegree = 1.00 \times \sin \theta_2 \\
\sin \theta_2 = \frac{1.50 \times 0.28}{1.00} \\
\sin \theta_2 = 0.42\\
\theta_2 = 25 \textdegree
}
$$
Total Internal Reflection
When travelling from optically dense to less there is the possibility that light is totally internally reflected and does not leave the medium.
This occurs when light is incident on the boundary with an angle above the critical angle which is defined below.
Critical Angle:
The angle in the less dense medium is 90 degrees at the critical angle so
$$
\displaylines{
n_{medium} \times \sin \theta_c = n_{air} \times \sin 90 \textdegree \\
\sin \theta_c = \frac{1}{n_{medium}} \\
}
$$
Example:
$$
\displaylines{
\sin \theta_c = \frac{1}{1.50} \\
\sin \theta_c = \frac{2}{3} \\
\theta_c = 41.8 \textdegree
}
$$
For more complicated boundaries go back to Snell's Law
For example the water - glass boundary has a critcal if light travels from glass to water.
Critical Angle glass to water:
$$
\displaylines{
n_1 \times \sin \theta_1 = n_2 \times \sin \theta_2 \\
1.50 \times \sin \theta_c = 1.33 \times \sin 90 \textdegree \\
\sin \theta_c = \frac{1.33 \times \sin 90 \textdegree}{1.50} \\
\sin \theta_c = 0.89 \\
\theta_c = 62.5 \textdegree
}
$$
Optic Fibre
Optic fibres work by trapping light inside very thin fibres and transmitting signals over long distances with low attenutation.
The cladding core boundary is based on total internal reflection with a high critical angle as the two transparent media have very similar refractive indicies.
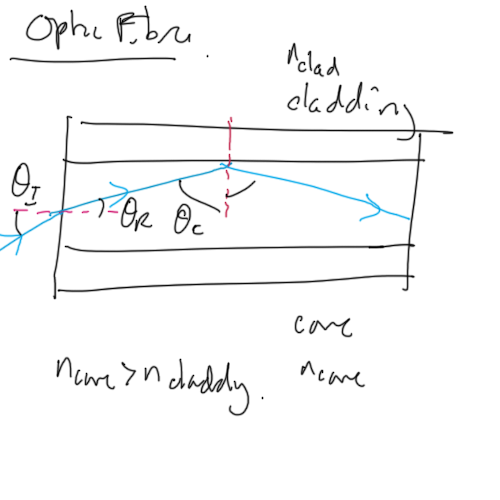
If the cladding has n = 1.50 and core has refractive index = 1.53, then the critical angle at the boundary is
$$
\displaylines{
n_1 \times \sin \theta_1 = n_2 \times \sin \theta_2 \\
1.53 \times \sin \theta_c = 1.50 \times \sin 90 \textdegree \\
\sin \theta_c = \frac{1.50}{1.53} \\
\sin \theta_c = 0.98\\
\theta_c = 78.6 \textdegree
}
$$
Multi-modal dispersion
Given an optic fibre with cladding and core as above there are still a range of possible angles that can be transmitted through the fibre.
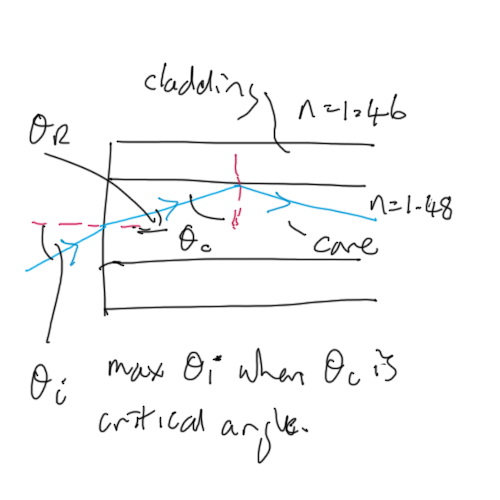
If the cladding has n = 1.46 and core has refractive index = 1.48, then the critical angle at the boundary is
$$
\displaylines{
n_1 \times \sin \theta_1 = n_2 \times \sin \theta_2 \\
1.48 \times \sin \theta_c = 1.46 \times \sin 90 \textdegree \\
\sin \theta_c = \frac{1.46}{1.48} \\
\sin \theta_c = 0.986\\
\theta_c = 80.57 \textdegree
}
$$
The maximum angle of incidence will be determined by the angle of refraction to produce the critical angle at cladding core boundary.
So angle of refraction \( \theta_R\) depends on the critical angle as:
$$
\displaylines{
\theta_R = 90\textdegree - \theta_C \\
\theta_R = 9.43 \textdegree \\
}
$$
So now the angle of incidence must be given by:
$$
\displaylines{
n_1 \times \sin \theta_1 = n_2 \times \sin \theta_2 \\
1.00 \times \sin \theta_i = 1.48 \times \sin 9.43 \textdegree \\
\sin \theta_i = 1.46 \times 0.164 \\
\sin \theta_i = 0.242 \\
\theta_i = 14.03 \textdegree
}
$$
So the range of angles that can be transmitted by the fibre are 0 to 14.03 degrees.
Given the fibre is 20 km long, find the maximum delay in the signal transmitted because of the different paths allowed down the fibre. This is multi-modal (path) dispersion.
First consider the shortest path:
$$
\displaylines{
\text{time of transit} = \frac{\text{distance}}{\text{speed}} \\
\text{time} = \frac{20 000 \times 1.48}{3 \times 10^8} \\
\text{time} = 9.87 \times 10^{-5} \; \text{s} \\
}
$$
Second consider the longest path:
$$
\displaylines{
\text{time of transit} = \frac{\text{distance}}{\text{speed}} \\
\text{time} = \frac{20 000 \times 1.48}{3 \times 10^8 \times \cos 9.43 \textdegree} \\
\text{time} = 10.01 \times 10^{-5} \; \text{s} \\
}
$$
So delay in transit is \( \Delta t = 1.35 \micro \text{s} \)
This puts a definite limit on the frequency of signals that can be transmitted by this fibre.
$$
\displaylines{
\text{max frequency} = \frac{1}{\text{time period}} \\
\text{max frequency} = \frac{1}{1.35\micro\text{s}} \\
\text{max frequency} = 741 \text{kHz} \\
}
$$
Refractive index as function of frequency
The refractive index of glass depends on frequency.
$$\begin{array}{|c|c|} \hline \text{wavelength} & \text{refractve index} \\ \hline
640 \; \text{nm} & 1.50917 \\ \hline
580 \; \text{nm} & 1.51124 \\ \hline
509 \; \text{nm} & 1.51534 \\ \hline
486 \; \text{nm} & 1.51690 \\ \hline
434 \; \text{nm} & 1.52136 \\ \hline
\end{array}$$
So the speed of light in glass depends the frequency. So the speed for blue and red light in glass is different.
$$
\displaylines{
\text{blue light speed} = \frac{3 \times 10^8}{1.51690} \\
\text{blue light speed} = 1.978 \times 10^8 \; \text{m/s} \\
}
$$
$$
\displaylines{
\text{red light speed} = \frac{3 \times 10^8}{1.50917} \\
\text{red light speed} = 1.988 \times 10^8 \; \text{m/s} \\
}
$$
This means red light is refracted less than blue everything else being the same.
Dispersion of white light
Each colour or frequency within white light is refracted by different amounts. The higher the frequency the more light is refracted.
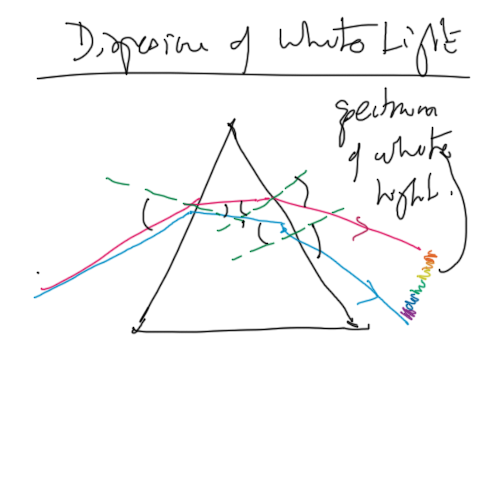
The effect is to split the colours of white light up. The example about is the classic way to do this using a 60 degree glass prism.
Example: White light incident on a 60 degree prism with indicent angle 30 degrees to the normal. Trace path of blue () and red (640 nm) light through the prism.
Red light (640 nm):
$$
\displaylines{
n_1 \times \sin \theta_1 = n_2 \times \sin \theta_2 \\
1.00 \times \sin 30 \; \textdegree = 1.50917 \times \sin \theta_g \\
\sin \theta_g = \frac{0.50}{1.50917} \\
\sin \theta_8 = 0.331 \\
\theta_g = 19.3 \textdegree
}
$$
Blue light (434 nm):
$$
\displaylines{
n_1 \times \sin \theta_1 = n_2 \times \sin \theta_2 \\
1.00 \times \sin 30 \; \textdegree = 1.52136 \times \sin \theta_g \\
\sin \theta_g = \frac{0.50}{1.52136} \\
\sin \theta_8 = 0.329 \\
\theta_g = 19.2 \textdegree
}
$$
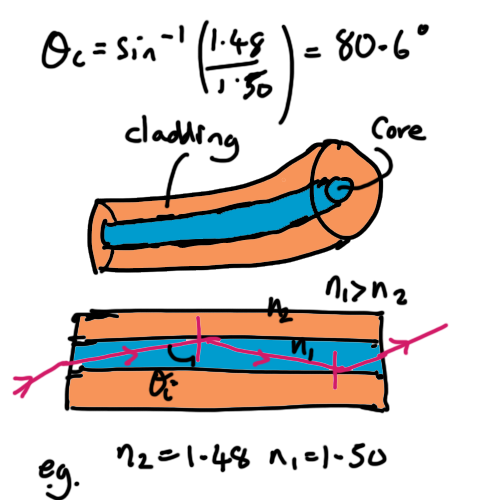
Optic fibres send signals over long distances. Any time difference over such distances causes a blurring out of the signal. This is highly problematic for modern digital technology.
If we introduce a time delay \( \Delta t \) then for a fibre length \( l \) then there will be a limit of the frequency of the signal we can send
$$ f_{limit} = \frac{1}{\Delta t} $$
Modern signals need to be stable up to 3 GHz so
$$ \Delta t = \frac{1}{3 \times 10^{9}} $$
$$ \Delta t = 0.33 \text{ ns}$$
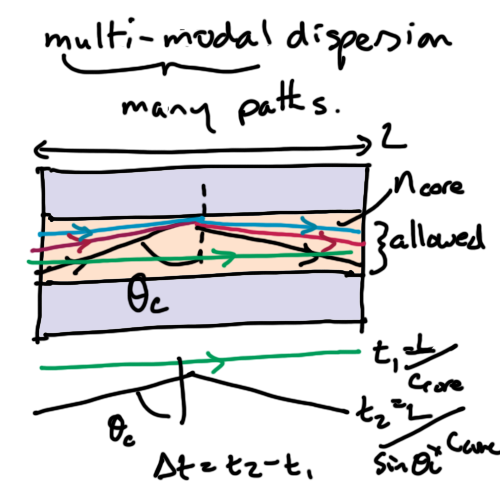
Multi-modal dispersion refers to the many allowed paths down a fibre that give rise to a time delay.
If we take the critical angle to be \( \theta_c \) then the time difference between the fastest and slowest routes through is
$$ t_{slow} - t_{fast} = \frac{\frac{L}{\sin\theta_c}}{c_{core}} - \frac{L}{c_{core}}$$
$$ t_{slow} - t_{fast} = \frac{L}{c_{core}} \times (\frac{1}{\sin\theta_c} - 1) $$
$$ t_{slow} - t_{fast} = \frac{L}{c_{core}} \times (\frac{1}{\sin\theta_c} - 1) $$
$$ t_{slow} - t_{fast} = \frac{L}{c_{core}} \times (\frac{n_{core}}{n_{cladding}} - 1) $$
so if \( n_{core} = 1.48 \text{ and } n_{cladding} = 1.46 \)
$$ \Delta t = \frac{L}{c_{core}} \times 0.0137 $$
so for fibre L = 2 km
$$ \Delta t = \frac{2000 \times 1.48}{3 \times 10^8} \times 0.0137 $$
$$ \Delta t = 0.135 \mu s $$
The thinner the fibre the lower the possible delay is as the transmission angle approaches the straight through path.
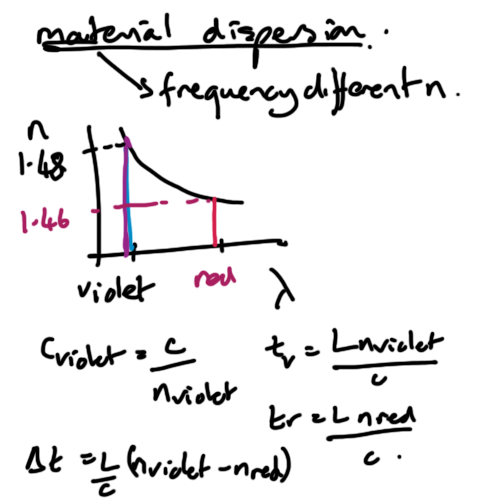
If the refractive index depends on the frequency or colour of light passing through the material then it wil introdcue a delay depending on the range of frequencies beign transmitted.
So it is best to use a monochromatic light signal for transmission.












