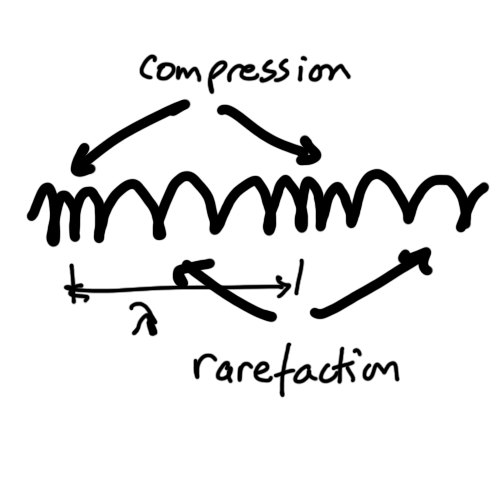
Longitudinal waves are waves in which the displacement on the medium is parallel to the direction of the wave through the medium.

Examples are: waves on a slinky spring, seismic p-waves and sound waves in air.

Transverse waves are waves in which the displacement of the medium is perpendicular to the motion of the wave through the medium.

The entire electromagnetic spectrum are transverse and all have the wave speed equal to the speed of light in a vacuum.

Transverse waves are plane polarised if the direction of oscillation is in one plane only.

Unpolarised waves have multiple random orientations.

laser light is always plane polarised. light from a filament lamp is unpolarised.

reflection of light always polarises the reflected light.

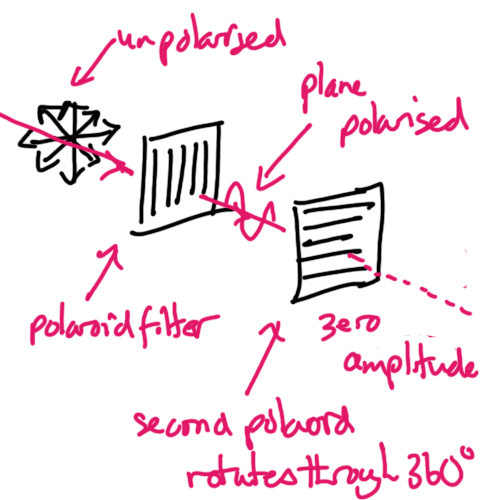
when the second polaroid is rotated the amplitude of light seen is a minimum twice when the polaroid filters are crossed.

NOTE: longitudinal waves can never be polarised.

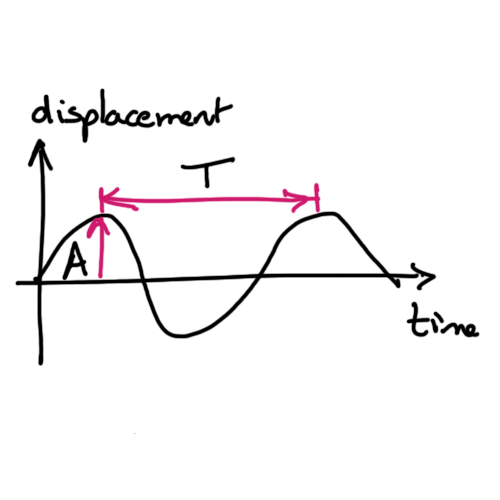
$$ y = A \sin {(2 \pi f t)} $$

Given angles taken to be in radians, then on cycle occurs between \( t=0 \text{ and } t=T \text{ which is } t=\frac{1}{f} \).

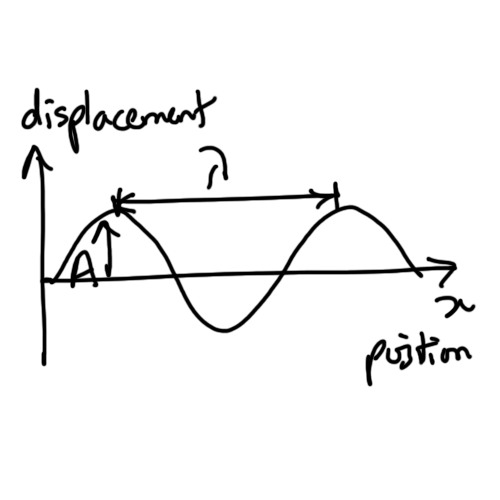
$$ y = A \sin {(\frac{2 \pi x}{\lambda})} $$

Again with angle measured in radians one complete cycle is from \( x=0 \text{ and } x= \lambda \)

Combining the two equations and allowing for an arbitary phase difference \( \phi \), then we can write out the complete soltion for a progrssive wave as below.

$$ y = A \sin {(\frac{2 \pi x}{\lambda} + 2 \pi f t + \phi)} $$

Wavelength is the distance between to exactly similar and adjacent positions on the wave.

Amplitude is the maximum displacement from equilibrium or rest position.

Time Period is the time for one complete cycle.

Frequency is the number of complete cycles per unit time.

Wave speed is the speed at which energy passes through the medium, often described as the speed of a wavefront.

$$ c = f \lambda $$

Speed of sound waves in air is usually taken as 340 m/s at sea level.

Speed of light in air is taken to be \(3 \times 10^8 \) m/s

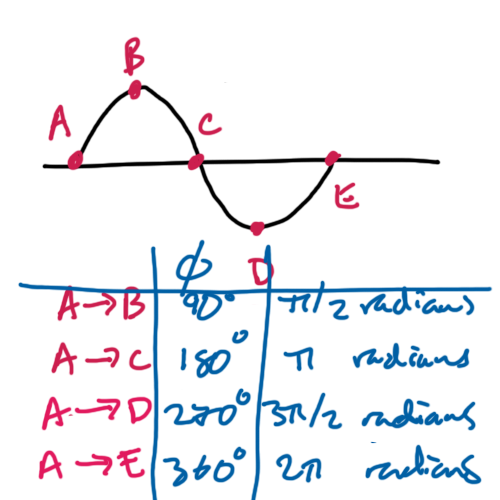
The phase difference between two points on the same wave is expressed as an angle. 360 degrees represents one complete cycle. In radians \( 2 \pi \) represents one complete cycle.

Examples of phase difference are shown below

It is very important to recognise in phase as 0 or 360 degrees difference. If this is the phase difference then the two points are at exactly the same point in the wave.

Also out of phase means 180 degrees or \( \pi \) radians. If this is the phase difference between two points then the displacement of one wave will always the negative displacement of the other wave.

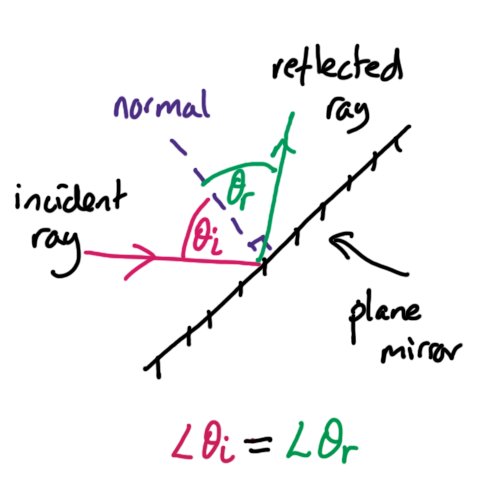
There are two laws of reflection:

1. The incident ray, the reflected ray and the normal are in the same plane.

2. The reflected angle measured from the normal is equal to the reflected angle measured from the normal.

Using this the properties of the reflected image can be determined. This is generally not covered at A-level.

However, understanding the normal is absolutely vital to progress beyond a descriptive stage.

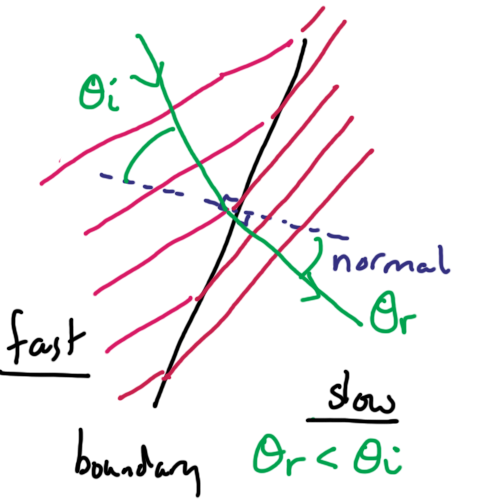
Refraction occurs when waves pass from one medium to another and the speed changes. This will lead to a change in direction if the waves are incident at an angle to the normal with the boundary between the two media.

In a simple example: If light travels from air to glass, it slows and bends towards the normal.

The greater the change in speed the more the waves will change direction.

Given the frequency of a wave is determined by the source, if a wave slows down then its wavelength must decrease.

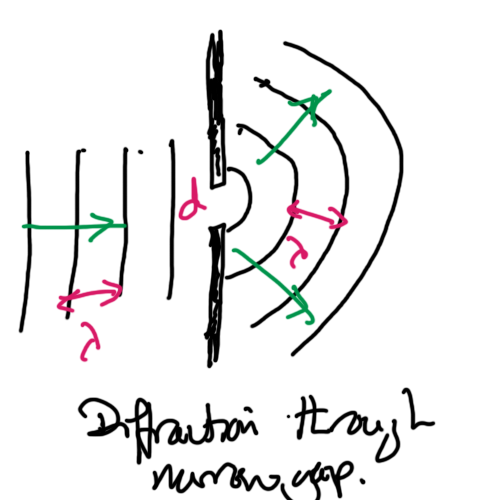
Diffraction occurs when plane waves incidnet on a narrow gap emerge and spread out as if from a point source.

This is really the condition for maximum diffraction to occur given the wavelength is equal to the gap.

The pattern for single slit diffraction is actually more complex than this but it is very useful to learn the condition for maximum diffraction.

$$ d = \lambda $$

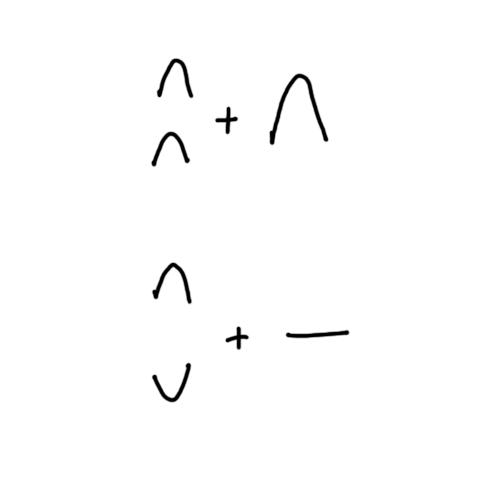
When two waves meet the resulting displacement is the vector sum of the displacements of the waves (e.g. peak meets peak).

This means that waves can cancel out if they meet such that the displacement of one wave is the negative displacement of the other wave (e.g. peak meets trough).

This is an extremely important idea and distinguishes a wave description from a particle description. Particles can not cancel (unless they annhiliate).

Mathematically the displacement is the sum of the displacements so:

$$ y = A_1 \sin{(\frac{2 \pi x_1}{\lambda} + 2 \pi f t)} + A_2 \sin{(\frac{2 \pi x_2}{\lambda} + 2 \pi f t + \phi)} $$

But we can ignore differences in time as we would observe the waves simultaneously so:

$$ y = A_1 \sin{(\frac{2 \pi x_1}{\lambda})} + A_2 \sin{(\frac{2 \pi x_2}{\lambda} + \phi)} $$

And if we assume both sources are in phase and the amplitude of each wave is equal when they meet then:

$$ y = A ( \sin{(\frac{2 \pi x_1}{\lambda})} + \sin{(\frac{2 \pi x_2}{\lambda})} ) $$

So if \(x_1 - x_2 = n \lambda \) then we get:

$$ y = 2 A \sin{(\frac{2 \pi x_1}{\lambda})} $$

Or if \(x_1 - x_2 = \frac{\lambda}{2}(2n -1) \) where n is an integer then:

$$ y = 0 $$

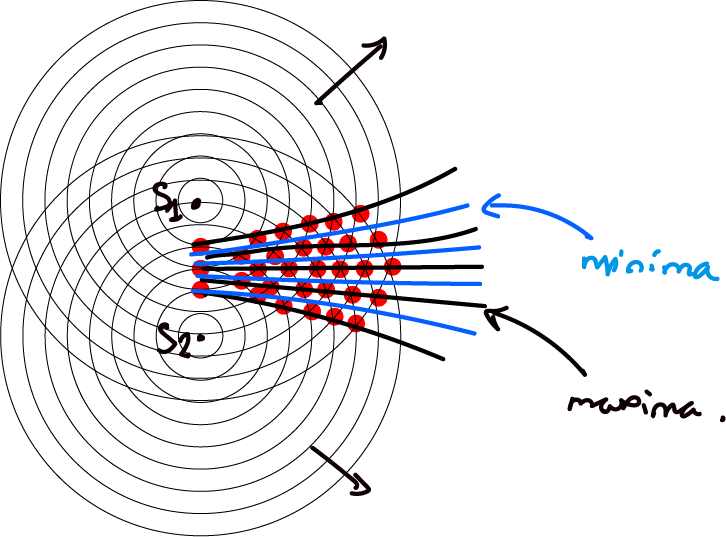
Two wave sources in phase are emmitting circular wave fronts at the same frequency and wavelength in water.

When the wave fronts meet they interfere constructively creating a region of high amplitude. Averaged over time this becomes the loci of the maxima spreading out from the sources.

Between the maxima are the minima where displacement is zero at all times.

The path difference from the sources to any point determines whether a maxima or a minima is observed.

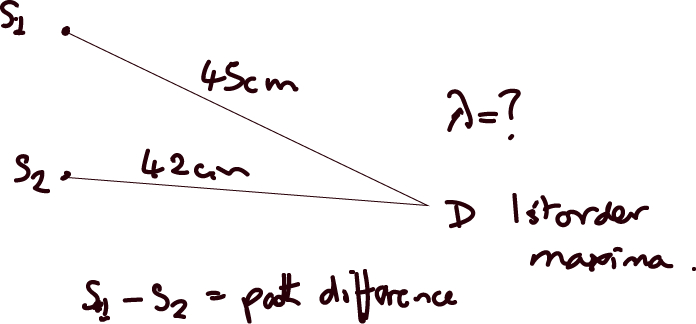
$$ \text{path difference for maxima} = n\lambda $$

$$ \text{path difference for minima} = (2n+1)\frac{\lambda}{2} $$

The wavelength above is given by:

$$ S_1 D - S_2 D = \lambda $$

$$ \lambda = 3 \text{cm} $$