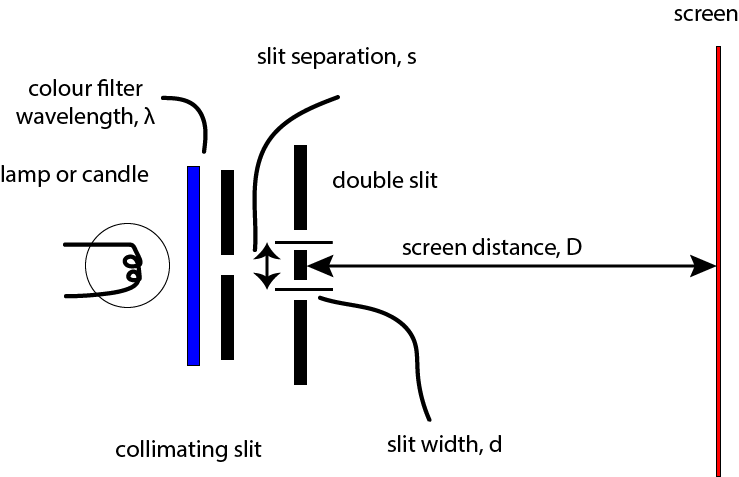
The diagram shows a typical arrangement for Young's Double Slits Experiment.
NOTE: Each slit has to be as narrow as possible but still wide enough to let sufficient light through. The slit width is typically 0.2 mm.
The slit separation needs to be very close to ensure the diffraction patterns from each separate slit ahve a chance of overlapping to produce the interference pattern. The slit separation is typically s = 0.5 mm.
The screen distance is between 0.5 m and 2 m typically.
The wavelength of light is in the visible range. A red laser is close to 650 nm. A sodium lamp has wavelength 589 nm. Otherwise it will depend on the filter used.
NOTE: An interference pattern can be observed with white light but it is much less clear.
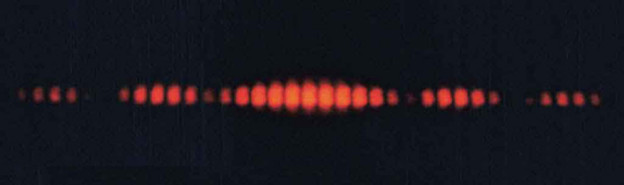
The pattern observed above is complicated as it includes the effects of diffraction through a single slit.
However, the observed pattern close to the central maxima is clear.
Equally spaced bright and dark fringes.
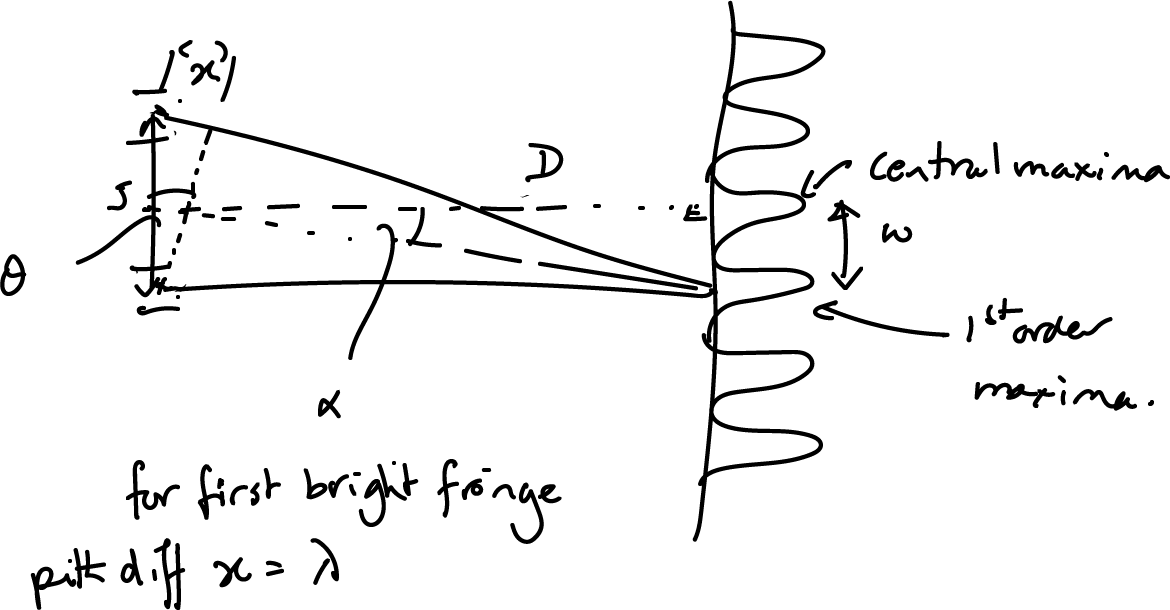
The path difference x for the first bright fringe away from the central maxima is \( x = \lambda \).
$$ \sin\theta = \frac{x}{s} $$
$$ \sin\theta = \frac{\lambda}{s} $$
The fringe separation from central maxima to first bright fringe is w.
$$ \tan\alpha = \frac{w}{D} $$
So assuming similar triangles and small angles
$$ \frac{\lambda}{s} = \frac{w}{D} $$
The path difference x for the first bright fringe away from the central maxima is \( x = \lambda \).
$$ \sin\theta = \frac{x}{s} $$
$$ \sin\theta = \frac{\lambda}{s} $$
The fringe separation from central maxima to first bright fringe is w.
$$ \tan\alpha = \frac{w}{D} $$
So assuming similar triangles and small angles
$$ \frac{\lambda}{s} = \frac{w}{D} $$

The interference pattern for white is more complicated than the monochromatic interference patterns below.
The central maxima is and then the first bright fringe goes from blue to red and begins to merge into the second bright fringe.
After a small number of bright fringes they begin to overlap substantially and it is hard to distinguish the bright fringe any more.