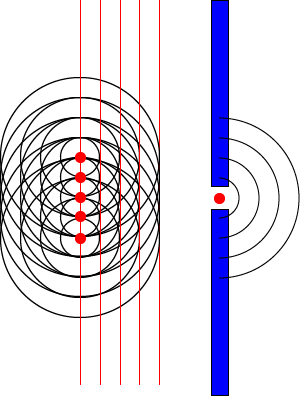
As can be seen above the diffraction pattern is complicated.

The central maxima is surrounded on both sides by maxima and minima.

The narrower the slit the wider the central maxima. This is a key idea.

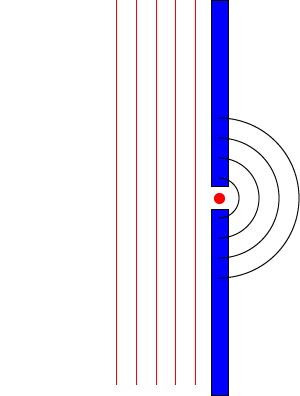
The pattern above is for the case when the slit width is four times the wavelength \( d = 4\lambda\).

In this case the first minima occurs at \( \sin\theta = \frac{\lambda}{d} = 0.25\)

For any slit the first minima occurs at

$$ \sin\theta = \frac{\lambda}{d} $$

for small angles (in radians)

$$ \sin\theta \approx \theta $$

Condition for first minima becomes

$$ \text{first minima at } \theta = \frac{\lambda}{d} $$

and the angular width of the central maxima is

$$ \text{anglar width of central maxima} = \frac{2\lambda}{d} $$

If the slit width equals the wavelength then the first minima occurs at

$$ \theta = \frac{\pi}{2} $$

which means light from the central maxima spreads out completely in front of the slit approximating a circular wave front.

Maximum diffraction occurs when

$$ d = \lambda $$

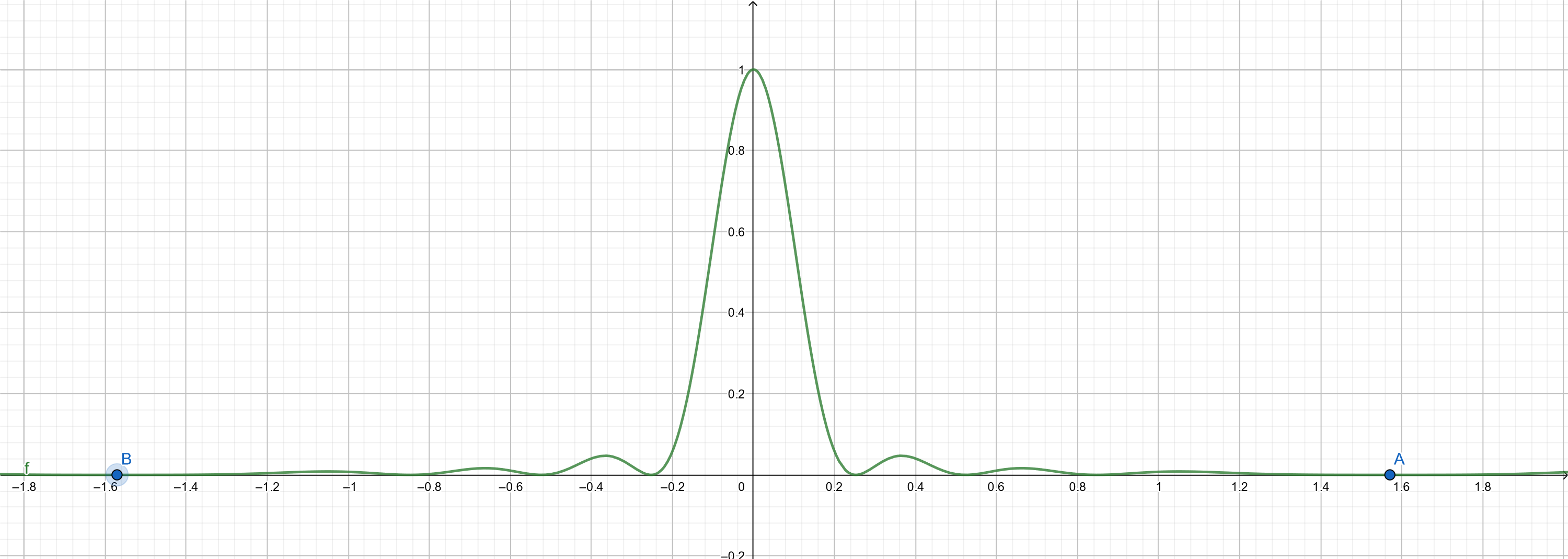
NOTE: Diffraction patterns are best understood by considering the condition for the first minima.

This occurs when light is totally cancelled out.

This is the classic way to distinguish wave phenomena. This can not be explained by a particle description. This is important when looking at electron diffraction and wave particle duality.

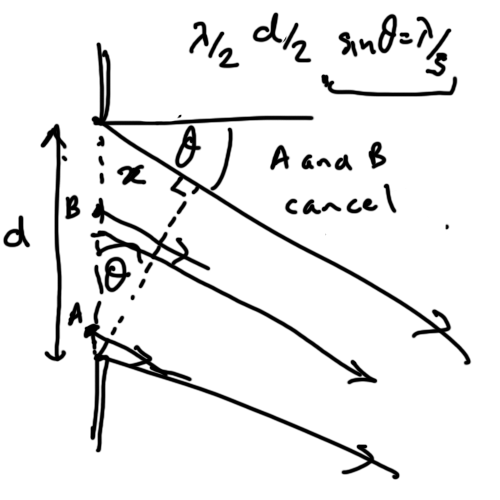
To explain the first minima we have to consider a ray in the lower half of the slit from A.

This must be cancelled out by a ray in the top half for there to be total cancellation.

We take that ray to be B and make sure that B is out of phase (\( \pi \) radians) with A.

If they are out of phase then

$$ \sin\theta = \frac{\frac{\lambda}{2}}{\frac{d}{2}} $$

$$ \sin\theta = \frac{\lambda}{d} $$

NOTE: This means for every ray in the bottom half there is a ray in top half exactly out of phase and hence we get total cancellation.

The condition for the first minima is then

$$ \lambda = d \sin\theta $$

Above is the emission spectrum of hydrogen viewed through a diffraction grating. This is a real application of the diffraction grating analysing the spectra of elements etc - spectroscopy.

A diffraction grating can be thought of as an extension of the double slit experiment with two slits replaced by hundreds of slits.

A typical grating will have 500 lines per mm. This has the effect of sharpening and spreading out the maxima and making the minima near perfect cancellations inbetween the maxima.

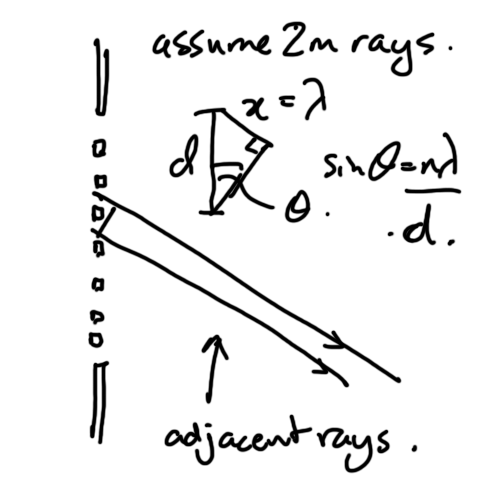
In the grating shown above we assume there are 2m lines and rays so that we can look at them in pairs.

We then look for the condition for there to be a maxima such that each pair add constructively - phase difference \( 2\pi\).

In this case the path difference for the first maxima is \( \lambda \).

$$ \sin\theta = \frac{\lambda}{d} $$

In general, for the nth maxima

$$ \sin\theta = \frac{n\lambda}{d} $$

Usually written as

$$ d\sin\theta = n\lambda $$

NOTE: because there are many lines if the angle is only slightly away from the condition for a maxima there will be near total cancellation.

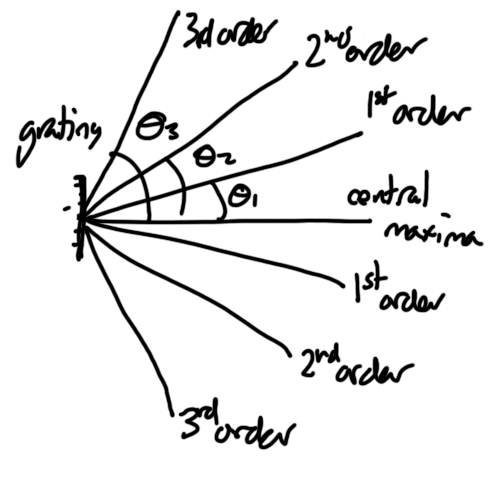
If the wavelength of the monochromatic light source is 600 nm and the grating has 500 lines per mm is find the angles for all the maxima beyond the central maxima.

$$ d = \frac{1\times10^{-3}}{500} $$

$$ d = 2\times10^{-6} \; m$$

$$ \sin\theta = \frac{n\lambda}{d} $$

$$ \sin\theta = \frac{n 6\times10^{-7}}{2\times10^{-6}} $$

$$ \sin\theta = n \times 0.3 $$

$$ \theta = 19.4\deg \text{(n=1), } 41.0\deg \text{(n=2) and } 71.3\deg \text{(n=3)} $$

NOTE: The maximum order visible is given by

$$ \sin{\frac{\pi}{2}} = n \frac{\lambda}{d}$$

$$ n = \frac{d}{\lambda} $$

Always take the least integer value.

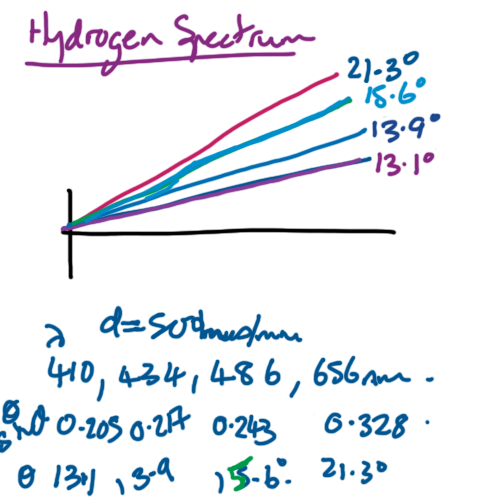
Hydrogen has four visible lines at wavelengths 410 nm, 434 nm, 486 nm and 656 nm.

If we take the spectrum for a grating with 500 lines per mm then

$$ d = 2 \times 10^{-6} \; m $$

So for order n = 1

$$ \sin\theta = \frac{\lambda}{2 \times 10^{-6}} $$

which gives \( \theta = 13.1 \degree \) for wavelength 410 nm

whilst \( \theta = 21.3 \degree \) for wavelength 656 nm

red lines are diffracted more than blue.

For second order maxima we get

$$ \sin\theta = \frac{2\lambda}{2 \times 10^{-6}} $$

So for wavelength 410 nm order two is at 26.9\( \degree\)

and for wavelength 656 nm order two is at 45.6\( \degree\)

For the 3rd order maxima the 656 nm line is at 88.9\( \degree\)

The fourth order maxima will work for the first three lines but the red line will not show up for the fourth order as \( \sin\theta \gt 1\)